The Quantum Field Theory of Interactions

A Theory Beyond the Standard Model

to explain the origin of the fundamental fermions.

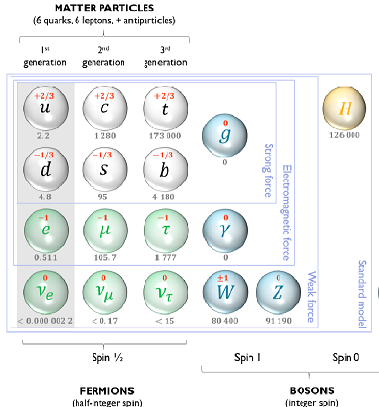
This theory, currently being researched by Nova Software, Inc., has the goal of explaining how the known stable fundamental fermions* arise from the three known fundamental particle interactions. The Standard Model assumes the existence of the observed fundamental fermions, and then is extremely successful in predicting the physics that ensues. The major tennets of its theoretical framework, quantum field theory (QFT) and the local gauge invariance principle, do not, however, constrain the Universe to that particular set of fermions and their eigenvalues. Many others are possible within that framework. It's only experiment that picks out the particular set used in the Standard Model. One must go beyond the Standard Model to find the theory for these facts.

Numerous theories "Beyond the Standard Model" have been proposed over the years to rectify this and other limitations of the Standard Model. These theories often are based on additional symmetries and/or interactions (forces) and/or fields (particles) beyond those currently part of the Standard Model, while preserving the QFT & gauge invariance framework. Some mechanism is typically included to explain why the added element(s) are not already readily apparent to us. That mechanism must be overcome in experiments to confirm the predictions of the "new physics." This theory takes a somewhat different approach in that it attempts only to explain the origin of those fundamental fermions we already know, based on the possibility that those really are all that there are. Such a possibility is suggested by the numerous unsuccessful searches for additional fundamental fermions over the past five decades.

In that spirit this theory goes beyond the Standard Model in a different direction by postulating a revised form of quantum field theory and local gauge invariance. It adds a hypothesis that enhances the role of the internal symmetry groups' smooth manifolds and their U(1) X SU(2) X SU(3) product to the founding of space-time. The theory becomes more restrictive than the Standard Model in order to admit only the known stable fundamental fermions. The observed sets of the fundamental fermions* and bosons** then emerge as derived objects in a natural way from these hypotheses and their mathematical consequences, as does a simplified, natural form of cosmic inflation and a candidate particle for dark matter. These results insure that the theory is compatible with the Standard Model's successes while providing a new understanding of how its fermions originate, and possibly other new, heretofore unsuspected, testable results.

In its current form, in addition to QFT and the Standard Model, the Quantum Field Theory of Interactions draws most heavily on mathematical results from the theories of topological groups and manifolds, homotopy theory, Lie groups and Lie algebras and differentiable manifolds. When complete the theory will be made available through the usual outlets that disseminate physics research results, and by free download here to enable and encourage other researchers to further investigate its potential.

* Fermions: There are 12 distinct fermions (fields) based on mass alone. (Illustration above.) When the SU(3) color quantum numbers are taken into account there are 24 fundamental fermions with those 12 distinct masses. These 24 consist of 8 different sets of various strong, E&M, weak and global quantum numbers. These 8 sets are then replicated twice more at higher masses, for some as yet unknown reason that lies outside the Standard Model. These three otherwise identical mass levels, the generations or families of the fundamental fermions and anti-fermions, may be assigned additional pairs of generation "quantum numbers", such as +-1, +-2, +-3, to distinguish them. The ordinary matter in the Universe consists entirely of generation +1 fermions, without -1 anti-fermions. This absence of anti-fermions is also unexplained in the Standard Model, which is symmetric between the two types of fermions, and thus favors an approximately equal distribution of the two. The higher generation fermions and lower anti-fermions are short-lived, decaying ultimately into generation 1 fermions, so do not contribute significantly to the matter in the Universe.
Conservation of quark generation number holds for all the strong interactions of the quarks. Quark generation number is not conserved, however, by their weak interactions, which, oddly and unexplained, will only change a quark to a lower generation quark of differing electrical charge, but not to one of the same electrical charge: No evidence for a quark flavor (i.e. generation) changing weak neutral current has ever been found, although one is permitted in the model and has been entensively searched for. The weak interaction differs in that its higher generation leptons produce lower generation leptons of both the same and different electric charge states in a decay, thus also not conserving its own generation number.
Chirality is a binary property of a field closely related to its behavior under transformations between right and left handed coordinate systems, i.e. to parity changes. It is not even an approximately conserved quantum number for Standard Model fermions with mass, but is nonetheless crucial for understanding the weak interaction. In the Standard Model it primarily affects the fermion fields. It splits the 24 fermion fields into 48 left and right chirality fields that must be considered separately when specifying which field particpates in which interaction. The left-chirality fermion fields (and their right-chirality anti-fermions) are the only ones participating in the charged weak interaction, i.e that between chiral fermions of differing electric charge. The neutral current weak interaction does affect both chiralities of the fundamental fermions, but with different strengths, i.e. effective coupling constants, so also makes a distinction based on chirality. Put another way the charged weak interaction makes a 100% distinction based on chirality, (its right-chiral coupling is 0), while the neutral one works with both chiralities with differing non-zero couplings. That then results in 18 of those 48 chiral fermions (left-chiral quarks) responding to all three interactions, while 21 respond to two interactions (18 right-chiral quarks to the strong + EM, & 3 charged left-chiral leptons to weak + EM ), 6 respond to only one (3 left-chirality neutrinos only to the weak interaction; 3 right-chirality charged leptons only to the EM interaction), and 3 have no known interaction at all (right-chirality neutrinos). These 3 might be considered only theoretical artifacts used to balance the books of the Standard Model, without physical significance, as there is no practical way to confirm their existence. Their gravitational interaction, if they were to have a typical lepton mass, would be far too weak to detect. Gravity is approximately 10^-32 weaker than the weak interaction, as a pure number, without any unit of measure. Note that the above counts all double if we count anti-fermions in addition to their partners.
This property of the chirality preference of the weak interaction is allowed by the underlying formalisms of the Standard Model, QFT and gauge theory, but not required. Consequently it is not an a priori theoretical prediction of the Standard Model, but rather another feature introduced by hand to match observations.
The 100% chiral selectivity of the charged weak interaction causes it to not conserve parity 100%. Some unknown aspect of the weak interaction causes it to also violate CP conservation at the ~4% level in certain higher generation processes. This result is embodied phenomenologically in the CKM matrix supplement to the Standard Model. Both fermion and anti-fermion chiralities participate in the strong and EM interactions equally, so these two interactions exhibit no chiral, no parity preference. The Standard Model also allows for the strong interaction to violate CP conservation up to 100%, but it does no do so. Attempts, both theoretical and experimental, to remedy this disagreement have not been successful. It remains an open question, unresolved within the Standard Model. CPT is conserved by all the interactions, universally.
Experiment has determined that quarks, the strong or color interaction fundamental fermions, cannot be found in a free state. They can only exist bound to one another in colorless combinations such as red+green+blue, or red+anti-red etc. This fact, called color confinement, is at odds with QFT's dependence on the concept of a free particle, at a fundamental level. Not surprisingly color confinement has thus far not been proven theoretically, within the Standard Model, to be a property of the color interaction.
Another unexplained fact related to free particles is that the weak interaction eigenstates of its fundamental fermions differ from their mass eigenstates as free particles. These facts are summarized in two empirical matrices: The CKM matrix for the quarks and the PMNS matrix for the leptons. These 3x3 unitary matrices represent a rotation in the Hilbert space of states of these three generations of fermions between their two sets of eigenstates, the freely propagating ones and the weak interacting ones. The angles of rotation are derived from experiment, not theory, and are large for the leptons, but much smaller for the quarks. Neither matrix has a generally accepted theoretical derivation within today's Standard Model, which is not surprising since there is no explaination for the existence of the three generations either.
The fundamental fermions and anti-fermions all have spin of 1/2. All have a positive mass: Gravity makes no distinction between fermion and anti-fermion mass. These mass values cover a wide range of 1:10^10 or greater. Charged lepton generation masses approximately satisfy the empirical Koide mass formula. Quark generation masses depart from it significantly. Neutrino mass measurements have only established upper limits to date. Their masses are much much smaller than all the other fermions, and unmeasureable thus far. They are indicated to be non-zero by the experimental observation of neutrino generation oscillations in flight and basic quantum theory.
** Bosons: There are 4 fundamental vector boson fields (spin 1) required in the Standard Model by the principle of local gauge invariance. (Illustration above.) When the quantum numbers are taken into account these fields give rise to 12 vector boson particles: 8 vector bosons (gluons) mediate the strong interaction, 1 (photon) mediates the electromagnetic interaction, and 3 (W+- and Z0) mediate the weak interactions of the left-chiral fermions and right-chiral anti-fermions. The W- and W+ are each other's anti-particle. The Z0 boson, of zero hypercharge and being the zero isospin member of a weak isospin triplet, is its own anti-particle. The gluons are self-dual fields, each its own anti-particle. They carry only linearly independent combinations of the three color and three anti-color eigenvalues. The photon has no quantum numbers so is also a self-dual field and its own anti-particle. Gluons and photons mediate their interactions for both fermions and anti-fermions, of both chiralities. In addition the charged weak vector bosons, W- and W+, participate in the electromagnetic interaction by virtue of their unit electric charges, although they are not its primary carriers. This two-interaction property makes them unique among the vector bosons.
The other fundamental boson is the scalar Higgs boson (spin 0) which does not mediate any one of the three fundamental interactions and is of a vastly different character than the vector bosons of the fundamental interactions. The Higgs we observe today might best be called the reduced Higgs, without any electric charge or other quantum numbers, and thus its own anti-particle. It's a single particle remnant of the expanded Higgs particle, which was a weak isospin doublet and anti-doublet that existed only in the ultra-high energy, tightly compressed, fundamental particle plasma during the first few moments of the beginning of the Universe. When the Standard Model and data from cosmology and astrophysics are projected back to those moments they indicate that only the Higgs had rest mass. All the other particles, both fermions and bosons were constrained to be massless by their fundamental interactions, which all require the local gauge principle. This principle only gives relativistically correct results if the fields are massless. As the Universe rapidly expanded from its ultra-hot and compressed state the plasma cooled, and the average energy of the Higgs field eventually fell to the current value of 246 Gev and stabilized there. This stabilization was possible due to the specific fourth power functional form of the potential energy field created by the Higgs field in the Standard Model. The reduced Higgs field is unique among the fundamental particles in having that substantial non-zero average value (energy) throughout the Universe.
Due to this decline in average energy the expanded Higgs field underwent a quasi-phase transition (known as spontaneous symmetry breaking or hiding) that left only the single, self-dual, reduced Higgs field with 0 weak isospin. At the same time the four initial, massless, weak hypercharge and weak vector boson fields mixed (transformed) into the three curently observed weak interaction vector boson fields with rest mass, and into the single massles photon field and its associated electromagnetic interaction that we see today. This mixing is modeled as a unitary transformation of the boson fields to a new basis in the Hilbert space of states, a rotation of approximately 29 degrees in that space. At the same time the weak hypercharge values of the chiral fermions became quantized into various increments of +-1/3. The Standard Model does not predict these values, so the correct weak hypercharge values are inserted into the fermion fields by hand to agree with their observed electric charges and the Standard Model formula: Q = 1/2 Y + T3, in which Q = electric charge, Y = weak hypercharge, T3 = weak isospin 3rd axis projection.
Before the mixing there were 12 physical degrees of freedom among the five bosons: Two possible spin orientations of each for the four massless vector bosons, and four arbitrary real values for the isospin doublet complex-valued expanded Higgs field. After mixing there are still 12 physical degrees of freedom: Three possible spin orientations for the three weak vector bosons now that they have mass, two for the massless vector photon, and one arbitrary real-valued component of the reduced scalar Higgs field. Thus the Standard Model portrays the three weak vector bosons each gaining mass and consequently one more physical degree of freedom (spin orientation) at the expense of the expanded Higgs field phase-transitioning to the reduced Higgs and loosing thereby three degrees of freedom. Its initial fourth degree of freedom becomes the reduced Higgs, a real-valued field.
Fundamental fermion masses would violate Lorentz invariance in the Standard Model Lagrangian as a consequence of the equations of local gauge invariance principle. This principle creates the interactions with the correct symmetry goup association, so takes precedence and thus disallows those masses. To account for the fact that the electrically-charged fundamental fermions do have mass the Standard Model Lagrangian includes simple direct contact (Yukawa) interactions between the expanded Higgs field and a chirality mix of the fermion fields. These terms are not derived from any underlying theoretical basis, just inserted "by hand" again to match observations. After the Higgs phase transition these terms result in mass-like Dirac terms proportional to each electically charged fermion field and to the reduced Higg's stable vacuum expectation value. These terms in the Lagrangian imply that the electrically-charged fundamental fermions feel a drag from the ubiquitious non-zero Higgs field due to this constant interaction. This drag slows their motion, as though each has some non-zero rest mass: They no longer are able to travel at the speed of light. The values of these masses are all proportional to the reduced Higg's stable vacuum expectation value and a different arbitrary coupling constant for each fermion. Thus the actual mass values are not predicted by the Standard Model, but must also be inserted by hand into numerical calculations. The corresponding mass terms for the neutral neutrinos sum to zero. Neutrinos only acquire mass latter via the PMNS matrix, empirically, in order to agree with the observation of neutrino generation oscillations.
The gluon field does not have any weak chiral isospin interaction nor weak hypercharge, so could not interact directly with the expanded Higgs field. The photon field likewise has neither interaction, and only arose later as a consequence of the Higgs phase transition and boson field mixing. Consequently neither the gluon nor photon acquired mass from the Higgs phase transition, so they are the only fundamental particles that are massless and can travel at the speed of light. The Standard Model, however, does not allow for free gluons in today's Universe. All gluons must be bound in colorless hadrons with the confined quarks, so only the photon can actually be observed traveling at the speed of light.

Many other fundamental particles with a wide variety of properties have been proposed and have been or are being actively searched for. The above are the only ones unequivocally confirmed by the Particle Data Group thus far and thus are the main subjects for the Standard Model and the only ones for this new Quantum Field Theory of Interactions.

Summmary for a general audience: The current physics theory of the known fundamental particles, the Standard Model, explains extremely well how they interact via their strong, electromagnetic and weak interactions and the Higgs field. It does not, however, explain how the particular set of fundamental particles that we observe arises, in preference to all other possible such sets. These facts are inserted into the theory "by hand" from what we see, rather than being derived from fundamental hypotheses. The Quantum Field Theory of Interactions is being researched at Nova Software, Inc., to address this question, to see if there is a theory that can successfully explain those facts from new fundamental hypotheses. If successful the theory will be made available in the usual physics locations for such work, and at this site in the hope that others will find it a worthwhile subject for further study.